(Feladat azonosítója: mmk_201605_2r14f )
Témakör: *Geometria (Pitagorasz)
Az ABCD húrtrapéz oldalainak hossza: AB = 5 cm, BC = 2,5 cm, CD = 2 cm és DA = 2,5 cm.
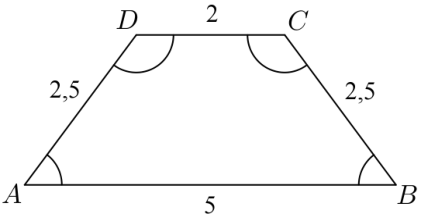
a) Számítsa ki a trapéz szögeit!
b) Határozza meg az ABC és ACD háromszögek területének arányát!
c) A trapéz belső szögeit egy-egy 5 mm sugarú körívvel jelöltük. Számítsa ki a négy körív hosszának összegét!
Megoldás
a) $\beta=\alpha \approx 53,13 ^{\circ};\quad \gamma=\delta=180^{\circ}-\beta \approx 126,87^{\circ}$
b) $\dfrac{T_{ABC}}{T_{ACD}}=\dfrac{5}{2}$
c) $ 10 \pi \approx 31,42 mm$