Az ABC háromszög körülírt körének egy $M$ pontjából bocsássunk merőlegest az AB és az AC oldalegyenesre, legyenek a talppontok $K$ és $L$! Hogyan kell megválasztani az $M$ pontot, hogy a KL távolság maximális legyen?

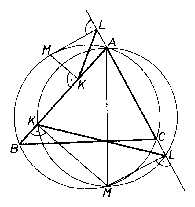
Mivel a $K$ és az $L$ pontokból az AM szakasz derékszögben látszik, ezért $K$ és $L$ az AM Thalész-körén van (1. ábra). E kör húrja, a KL az AM átmérőnél nagyobb nem lehet. Mivel AM Thalész-körének KL húrjához a BAC$\angle $ vagy $\pi -BAC\angle $ tartozik kerületi szögként, ezért $KL=AM\sin BAC\angle $. Így KL akkor maximális, ha AM is az, ha tehát $M$ az ABC háromszög körülírt körének $A$-val ellentétes pontja. A KL húr ekkor a BC oldallal azonos.
Megjegyzés: Megoldásunk során felhasználtuk, hogy az $M$ pont nem lehet azonos az $A$, $B$, $C$ csúcsok egyikével sem. Ez esetben ugyanis nincs értelme az AKM$\angle $ vagy az ALM$\angle $ látószögének. Ha $M$ a $B$ vagy $C$ csúcsok egyikével azonos, akkor is igaz, hogy $L$, illetve $K$ az AM átmérőjű körön van, ha pedig $M$ az $A$-val azonos, akkor $K$ és $L$ is az $A$-val esik egybe, azaz KL minimális.