Az AB szakasz mint átmérő fölé rajzoltuk a $k$ félkört. Legyen $C$ a $k$-nak $A$-tól és $B$-től különböző, tetszőleges pontja, $D$ pedig a $C$-ből AB-re bocsátott merőleges talppontja. Tekintsük a következő három kört ($k_1 $-et, $k_2 $-t és $k_3 $-at), amelyeknek AB közös érintője, $k_1 $ az ABC háromszögbe írt kör, míg $k_2 $ és $k_3 $ mindegyike érinti a CD szakaszt is, a $k$ félkört is. Bizonyítsuk be, hogy $k_1 $-nek, $k_2 $-nek és $k_3 $-nak van még egy közös érintője!

Elég belátnunk, hogy a $k_1 ,\;\,k_2 ,\;\,k_3 $ kör $O_1 ,\;\,O_2 ,\;\,O_3 $ középpontja egy $e$ egyenesen van. Ez az egyenes ugyanis közös szimmetriatengelyük, tehát az AB közös érintő $e$-re vonatkozó tükörképe szintén érinti mindhárom kört. Legyen a $k_i $ kör középpontja $O_i ,$ sugara $r_i ,$ AB-n levő érintési pontja $T_i \,(i=1,\,2,\,3),$ a $k$ félkör középpontja $O$, átmérője $c$. Azt fogjuk bebizonyítani, hogy $O_1 $ az $O_2 O_3 $ szakasz felezőpontja, vagyis hogy

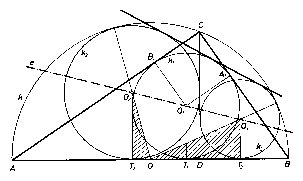
Feltehetjük, hogy -- a 1. ábra szerint -- $CB\le CA,$ ezért $D$ az OB szakaszon van, és legyen $OD=d;$ továbbá $k_2 $ a CDA, $k_3 $ a CDB derékszög tartományában van.

$k_2 $ érinti a CD szakaszt, ezért $T_2 D=r_2 ;$ érinti $k$-t, ezért $OO_2 =(c 2)-r_2 $. Az $OO_2 T_2 $ derékszögű háromszögben $OT_2 =\left| {d-r_2 } \right|,$ és így

Mivel $dABC derékszögű háromszög. Tehát

Hasonlóan az $OO_3 T_3 $ derékszögű háromszögben $OO_3 =(c 2)-r_3 ,\;\,OT_3 =d+r_3 ,$ Pitagorasz tétele alapján $r_3^2 +(2d+c)r_3 -(({c^2} 4}} \right. } 4)-d^2)=0,$ ennek pozitív gyöke

Tehát

ami könnyen adódik az ABC háromszögből, a $k_1 $ körhöz húzott érintőszakaszok egyenlőségéből. Ezzel (1)-et beláttuk. $k_1 $ érintőszakaszainak egyenlőségéből az is adódik, hogy

Felhasználva (1)-et és (3)-at

Ezzel a (2) állítást és így a feladat állítását is bebizonyítottuk.