(Feladat azonosítója: VF_000018 )
Témakör: *Geometria (kör, érintő)
Szerkesszünk háromszöget, ha adott a háromszög köré írt kör sugara, az oldalakat belülről érintő kör sugara és a háromszög egyik szöge.
Képzeljük a feladatot megoldottnak. Legyen az adott szög a háromszög köré írt kör középpontja $K$ és sugara$ r$, a beírt kör középpontja és sugara $\rho $. (1. ábra). A $BOC\Delta $-ből
A kerületi szögek tétele alapján a $K$ középpontú és $r$ sugarú körben tetszőleges $\alpha $ kerületi szög szárainak a körrel való metszéspontjai megadják a háromszög $BC=a$ oldalát. Az $O$ pont -- a fentiek szerint -- rajta van azon a BC köríven, melynek pontjaiból a BC távolság $ 90^{\circ}+\frac{\alpha }{2}$ szög alatt látszik és amely körív a BC oldalnak ugyanazon oldalán van, mint az $\alpha $ szög csúcspontja. E látószög-kör középpontja $P$ -vel jelölve, a középponti és kerületi szög közötti összefüggés alapján
vagyis az ABPC négyszög húrnégyszög és így $P$ pont a BC ív felezőpontja. Egy másik geometriai hely $O$-ra nézve a BC egyenestől $\rho $ távolságban a BC-vel párhuzamosan húzott egyenes, a BC egyenesnek ugyanazon az oldalán, mint az előbbi körív. A két mértani hely egyik metszéspontja a keresett $O$ pont. $O$ körül $\rho $ sugárral rajzolt körhöz a $B$ és $C$ pontokból szerkesztett érintők metszéspontja $A $(amely rajta van a köré írt körön) a keresett háromszög harmadik csúcspontja. (Általában két pontot kapunk $O$ számára, de mindkettő egybevágó háromszögekre vezet, tehát csak egy megoldásról beszélünk.) Határozzuk meg a megoldhatóság feltételeit. Jelöljük az $a$ oldal felezőpontját $A_1 $-gyel és a $PA_1 $ egyenesnek metszéspontját a látószög-körívvel, $Q$-val. Megoldás nyilván csak akkor van, ha $\rho \le A_1 Q$.
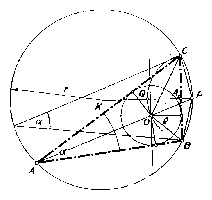
Mivel (1) alapján az $A_1 BP\angle =\frac{\alpha }{2}$, azért $A_1 P=\frac{a}{2}tg\frac{\alpha }{2}=\frac{a\sin \frac{\alpha }{2}}{2\cos \frac{\alpha }{2}}$ és $PQ=PB=\frac{a}{2\cos \frac{\alpha }{2}}$ amiből $A_1 Q=PQ-A_1 P=\frac{a}{2\cos \frac{\alpha }{2}}-\frac{a\sin \frac{\alpha }{2}}{2\cos \frac{\alpha }{2}}=\frac{a\left( {1-\sin \frac{\alpha }{2}} \right)}{2\cos \frac{\alpha }{2}}$. De $a=2r\sin \alpha =4r\sin \frac{\alpha }{2}\cos \frac{\alpha }{2}.$ és így $A_1 Q=2r\sin \frac{\alpha }{2}\left( {1-\sin \frac{\alpha }{2}} \right)$. Tehát megoldás csak akkor van, ha
Egyenlőség esetén $\rho =A_1 Q$ és a háromszög egyenlőszárú $\left( {b=c} \right)$. Állandó $r$ esetén a jobboldal akkor maximális, ha $\sin \frac{\alpha }{2}\left( {1-\sin \frac{\alpha }{2}} \right)$ maximális. Egy szorzat pedig, amelyben a tényezők összege állandó, akkor veszi fel a legnagyobb értéket, ha a tényezők egyenlők, vagyis $\sin \frac{\alpha }{2}=\frac{4}{2}$, amiből $\alpha =60^{\circ}$, és $\rho \le \frac{r}{2}$. $\rho $ maximális értéke tehát $\frac{r}{2}$ és ezt akkor veszi fel, ha $\alpha =60^{\circ}$ és azonkívül $\beta =\gamma =60^{\circ}$, vagyis a háromszög egyenlő oldalú.
2. Megoldás
Felhasználjuk ezt a tételt (1. osztályos tankönyv 1950-es kiadás, 285. oldal), mely szerint egy háromszög beírt és hozzáírt körének egy-egy közös külső érintő oldalon lévő két érintési pontjának távolsága egyenlő a harmadik oldallal, amely a fenti két kör közös belső érintőjének a külső érintők közé eső szakasza.
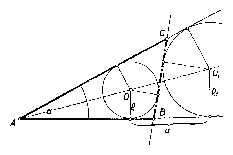
Eszerint a szerkesztés mente: a $BC=a$ háromszög oldal szerkesztése ugyanúgy történik, mint az 1 megoldásban. Felvesszük az $\alpha $ szöget és szerkesztünk egy $\rho $ sugarú, mindkét szárt érintő kört (1. ábra). Az egyik szögszáron az érintési pontól kiindulva felmérjük -- a szög csúcspontjától távololdó irányban -- az $a$ távolságot. Az így nyert pont lesz az említett tétel alapján a hozzáírt kör érintési pontja. A beírt és hozzáírt kör egy közös belső érintője metszi ki az $\alpha $ szög száraiból a $B$ és $C$ csúcspontokat. A megoldhatóság feltétele: a hozzáírt kör középpontját $O_1 $-gyel és sugarát $\rho _1 $-gyel jelölve, feladatunk csak akkor oldható meg, ha $\rho +\rho _1 \le OO_1 $. De
és így feltételünk
amiből $\rho \le \frac{a\left( {1-\sin \frac{\alpha }{2}} \right)}{2\cos \frac{\alpha }{2}}=2r\sin \frac{\alpha }{2}\left( {1-\sin \frac{\alpha }{2}} \right)$, ami megegyezik az 1. megoldásból nyert feltétellel.