Az ABC háromszög oldalainak hossza rendre AB = 5, BC = 6 és CA = 7 egység. Az AB oldal egy $P$ pontját a $B$ körül ráforgatjuk a BC oldalra (kapjuk így a $P_{1}$ pontot), ezt a $P_{1}$-et a $C$ körül AC-re ($P_{2})$, ezt a $P_{2}$-t pedig $A$ körül az AB-re ($P_{3})$. Ezt ismét $B$ körül BC-re ($P_{4})$, ezt $C$ körül AC-re ($P_{5})$ és végül ezt $A$ körül az AB-re($P_{6})$. Bizonyítsuk be, hogy $P_{6}$ egybeesik $P$-vel!

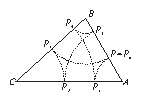
A forgatás a szakasz hosszán nem változtat, ezért BP = 5 -- AP = BP$_{1}$. CP$_{1}$=6 - (5 -- AP) = 1 + AP ($<$ 6) = CP$_{2}$, $P_{2}$ mindig az AC szakaszon van. AP$_{2}$ = 7 -- (1 + AP) = 6 -- AP = AP$_{3}$, a $P_{3}$ pont eshet a $B$ ponton túlra is. Ebben az esetben megtartjuk az eredeti forgásirányt, így elforgatottja sem lesz rajta a BC szakaszon, csak az egyenesén. (Előjeles távolságokkal számolunk.) BP$_{3}$ = 5 - AP$_{3}$ = AP -- 1 =BP$_{4}$ CP$_{4}$=6 - (AP - 1) = 7 - AP = CP$_{5}$ AP$_{5}$ = 7 -- (7 - AP) = AP = AP$_{6}$, azaz a $P_{6}$ egybeesik $P$-vel. Megjegyzés A feladathoz többféle megoldás is található a Bergengóc példatárban. (60. feladat)