(Feladat azonosítója: VF_000008 )
Témakör: *Geometria (magasság, tükrözés)
Bizonyítsuk be, hogy bármely háromszög magassági pontjának az oldalak felezőpontjára vonatkozó tükörképei a háromszög köré írt körön vannak.
Ha az egyik oldal középpontjára tükrözünk, akkor a magasság, tükrözési pont, a tükörképe és a kérdéses oldal végpontjai olyan négyszöget alkotna, melynek átlói felezik egymást, tehát parallelogrammát. Ennek a tükrözött pontba futó oldalai merőlegesek egy-egy háromszögoldalra, mert a parallelogramma velük párhuzamos oldalai a háromszög magasság, tükrözésai. Így a háromszög csúcsai és a magasság, tükrözéspont tükörképe olyan négyszöget alkotnak, melynek két szemközti szöge derékszög. Ez a négyszög tehát húrnégyszög. Így a háromszög köré írt kör átmegy a magasság, tükrözési pont tükörképén. A meggondolás hegyes és tompaszögű háromszögre egyformán alkalmazható.
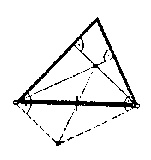
2. Megoldás
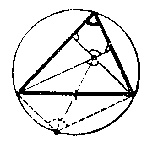
Eljárhatunk fordítva is. A magasság, tükrözéspontot összekötjük az oldal felezőpontjával és meghosszabbítjuk az egyenest a körig. Ekkor a keletkező metszéspontról kell megmutatni, hogy az a magasság, tükrözési pontnak a felezőpontra vonatkozó tükörképe, vagyis, hogy az oldal középpontja felezi a magasság, tükrözési ponttól a körig terjedő szakaszt is. Ez esetben az e két pont és a kérdéses oldal végpontjai által meghatározott négyszög parallelogramma. Ezt fogjuk bebizonyítani. Az egyíves szögek, mint csúcsszögek egyenlők. A felső $ 180^{\circ}$-ra egészíti ki a háromszög kövéríves szögét, mert e szögek szemköztes szögei egy olyan négyszögnek, melynek másik két szöge derékszög. A kövéríves szöget a szaggatott ívű szög is $ 180$ fokra egészíti ki, mert olyan kerületi szögek, melyeknek ívei egymást teljes körré egészítik ki. Így a kérdéses négyszögről azt tudjuk,hogy két szemközti szöge egyenlő és az ezek csúcsát összekötő átló felezi a másik átlót. Az ilyen négyszög valóban parallelogramma.
3. Megoldás
Ismerünk (az I. gimn. új tankönyvéből pl.) egy hasonló tételt: A magasság, tükrözési pontnak az oldalakra vonatkozó tükörképei a körülírt körön vannak. Ezt felhasználva is bizonyíthatjuk a tételt. Azt kell felhasználnunk, hogyha egy pontot egymásután tükrözünk két egymásra merőleges egyenesre, akkor a pontnak a tengelyek metszéspontjára vonatkozó tükörképéhez jutunk. Esetünkben a magasság, tükrözési pontnak az oldalra vonatkozó tükörképét még az oldal középmerőlegesére kell tükröznünk. Ez az egyenes azonban átmegy a körülírt kör középpontján, s így tükörtengelye a körnek. Az ekörüli tükrözés tehát a középpontra vonatkozó tükörpontba, másrészt ismét a körülírt körön fekvő pontba viszi át a magasság, tükrözéspontnak az oldalra vonatkozó tükörképét.
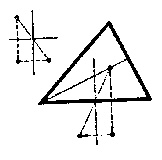
4. Megoldás
Rajzoljuk meg mindhárom tükörpontot. Az ezek meghatározta háromszög egybevágó az eredetivel és hozzá képest $ 180^{\circ}$-kal el van forgatva, mert úgy keletkezett az oldalfelezőpontok alkotta háromszögből, hogy azt a magasság, tükrözési pontból, mint középpontból kétszeresre nagyítottuk. Meg fogjuk mutatni, hogy a két háromszög oldalfelező merőlegesei egybeesnek, vagyis, hogy két-két egyenlő oldal végpontjai téglalapot határoznak meg. Vizsgáljuk a vastagított oldalt. Azok az egyenesek, amelyek ennek végpontjait kötik össze a másik két oldal középpontjára vonatkozó tükörképekkel, párhuzamosak és egyenlők a vastagított oldalra bocsátott magasság, tükrözésnak a háromszögcsúcs és a magasság, tükrözési pont közti szakaszával, mert ennek tükörképei egy-egy oldalközéppontra nézve. Így merőlegesek a vastagított oldalra. A kérdéses négyszög tehát valóban téglalap.
Megjegyzés. Rajzoljuk meg a körülírt kört és a magasság, tükrözési pontnak a ráeső hat tükörképét. Ha a kört most a magasság, tükrözési pontból felére kicsinyítjük, akkor az oldalra vonatkozó tükörképek a magasság, tükrözésok talppontjára fognak kerülni, az oldalközéppontra vonatkozó tükörképek pedig az oldalközéppontra. E hat pont tehát egy körön van. Ennél az összehúzásnál a háromszögcsúcsok a magasság, tükrözésokon a csúcs és magasság, tükrözési pont közti szakasz felezőpontjába fognak kerülni.
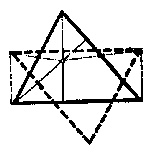
Ezekkel együtt 9 nevezetes pontot találtunk a háromszögben, melyek egy körön vannak. Ezt a kört a háromszög Feuerbach-féle körének nevezzük. A feles kicsinyítésből az is következik, hogy a Feuerbach-kör középpontja középpontja a magasság, tükrözéspont és a körülírt kör középpontja közti szakasznak is. Az e három ponton átmenő egyenest Euler-egyenesnek nevezik és megmutatható, hogy ezen rajta van a súlypont is. Az I. megoldásból a Feuerbach-körre vonatkozó állítások egy egyszerű bizonyítása is adódik. Rajzoljuk meg a magasság, tükrözésvonalakra eső pontok alkotta háromszöget és kössük össze az egyik oldal végpontjait a párhuzamos háromszögoldal középpontjával.
Ekkor e háromszögoldal és a magasság, tükrözéspont alkotta háromszögben meghúztuk mindhárom középvonalat. Így a szaggatott négyszög két szemközti szöge derékszög lesz, tehát a kis háromszög köré írt kör átmegy a nagy háromszög oldalainak középpontján. Az oldalközéppontot a kis háromszög szemközti csúcsával összekötő egyenes e körnek átmérője. Mivel ez a szakasz a magasság, tükrözés talppontjából is derékszög alatt látszik, így e talppont is a körön van.